$m=3$
半径1の円周上にある正 $m$ 角形のある一点から他の頂点への距離の積は $ m$ になります。
私が知ったのは このサイト です。
このブログ に簡単な証明があります
(10年以上前のブログですが、命題の 出展 も記されています。)
以下ブログより証明を引用させて頂きます。
$ \zeta =e^{2\pi i /m}$ とすると、 \[ X^m-1=\prod_{k=0}^{m-1}(X-\zeta^k) \tag{1}\] 両辺を $ X-1$ で割って \[ \sum_{i=0}^{m-1}X^i=\prod_{k=1}^{m-1}(X-\zeta^k) \] $ X=1$ として \[ m=\prod_{k=1}^{m-1}(1-\zeta^k)=\prod_{k=1}^{m-1}|1-\zeta^k | \] 左辺の複素平面での意味を考えれば、これで証明は終わりです。
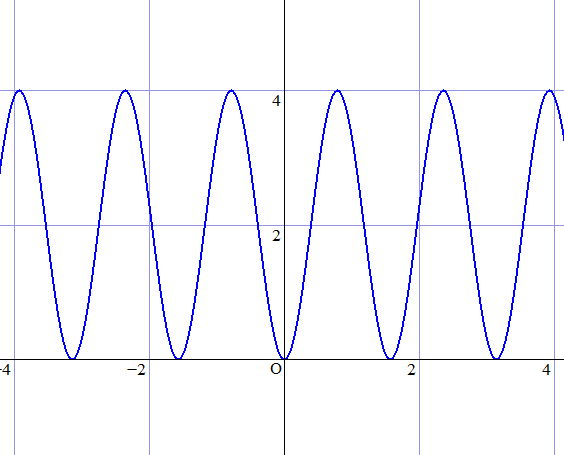
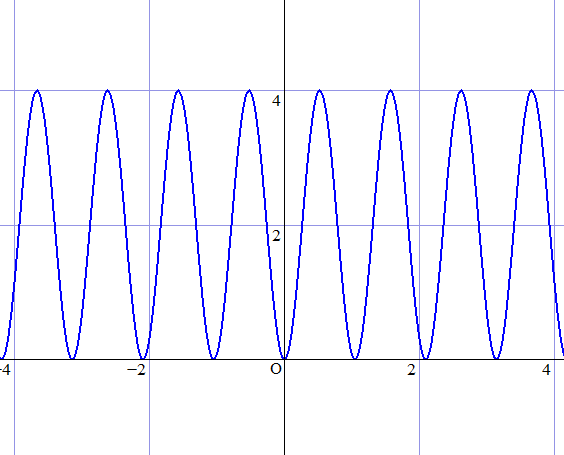
この話を見た時気になったのは、積を取る点から、距離を測る基準となる点が除外されていることでした。 もちろんその点を含めると、距離は $0$ なので、求める積も $0$ になってしまいます。 そこで距離を測る基準の点をずらして、例えば円周上の他の点にします。 そこから円周上のを含めた点たちへの距離の積を取ったらどんなグラフになるか。 GRAPESという簡単にグラフが描けるソフトを使って描いてみるとこんな感じになりました。
$m=2$

$m=3$

どうやら正弦曲線になるみたいです。
式にするとこんな感じの等式が成り立つ様子。
\[ \prod^{m-1}_{k=0}\left\{ \left( \cos 2x - \cos \frac{2k}{m}\pi \right)^2 + \left( \sin 2x - \sin \frac{2k}{m}\pi \right)^2 \right\} = 4\sin^2 mx \]
左辺を変形したところ、次のような等式が成り立てばよいことがわかりました。
(詳しくは5.補足(1)式変形)
\[ 2\sin (mx) = \prod^{m-1}_{k=0} 2\sin \left( x+\frac{k}{m}\pi\right) \tag{2}\]
元ネタと同様の議論によって最初の等式が示すことができました。
上の証明の(1)に $X=e^{2xi}$と代入すると、 \[ e^{2mxi}-1=\prod_{k=0}^{m-1}(e^{2xi}-e^{-2\pi i k/m})\] \[ e^{mxi} \cdot\left( e^{mxi}-e^{-mxi}\right) =\prod_{k=0}^{m-1} e^{\frac{mx-\pi k}{m}i}\cdot \left( e^{\frac{mx+\pi k}{m}i}-e^{-\frac{mx+\pi k}{m}i}\right)\] $ \sin\theta =(e^{\theta i}-e^{-\theta i})/2i$ より \[ e^{mxi} \cdot 2i\cdot \sin mx =\prod_{k=0}^{m-1} e^{\left( x-\frac{\pi k}{m}\right) i} \cdot 2i\cdot \sin \left( x+\frac{\pi k}{m}\right)\] \[ 2 \sin mx =i^{m-1}\exp\left(-mxi+\sum_{k=0}^{m-1}\left( x-\frac{\pi k}{m}\right) i\right)\times \prod_{k=0}^{m-1} 2 \sin \left( x+\frac{\pi k}{m}\right)\] ここで$\exp$の中身は、 \[ -mxi+\sum_{k=0}^{m-1}\left( x-\frac{\pi k}{m}\right) i=-\frac{\pi i}{2}\cdot (m-1)\] よって指数部分は$ \left(\exp \left(\frac{\pi i}{2}\right)\right)^{-(m-1)}=i^{-(m-1)}$なので、 \[ 2\sin (mx) = \prod^{m-1}_{k=0} 2\sin \left( x+\frac{k}{m}\pi\right)\] が成り立つ。(証明終わり)
ちなみに (2) の両辺を $x$ で割って $x\to 0$ の極限を取ると、wikipediaの三角関数の公式 に載ってる公式 \[ m = \prod^{m-1}_{k=1} 2\sin \left( \frac{k}{m}\pi\right) \] になります。最初に紹介したサイトでは、この等式が最初の命題を証明するための補題として証明されています。
証明された等式
\[ \prod^{m-1}_{k=0}\left\{ \left( \cos 2x - \cos \frac{2k}{m}\pi \right)^2 + \left( \sin 2x - \sin \frac{2k}{m}\pi \right)^2 \right\} = 4\sin^2 mx \]
の特殊な場合を考えた時、何が言えるでしょうか?
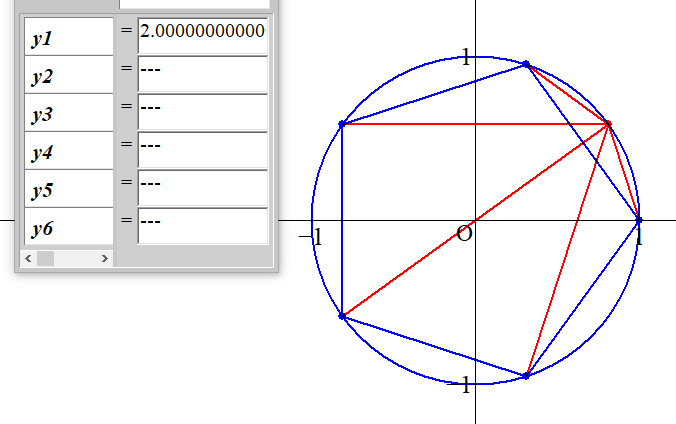
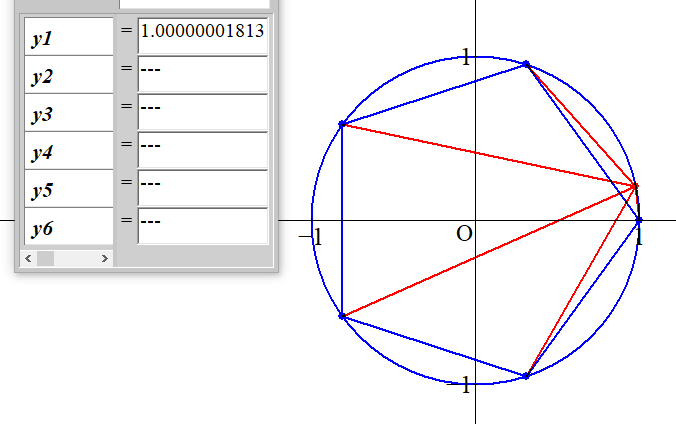
円周上に正$m$角形を配置し、正$m$角形の隣り合う頂点ABを結ぶ円弧を $ 2,\ 3,\ 4,\ 6$ 等分したとします。
頂点Aに一番近い等分点をそれぞれ $ P_2,\ P_3,\ P_4,\ P_6$ としましょう。
その点から、正 $m$ 角形のすべての頂点への距離の積は $m$ によらず、それぞれ
\[ 2,\ \sqrt{3},\ \sqrt{2},\ 1 \]
となります。
今回の話の元ネタは 『正 $m$ 角形の一つの頂点から他の頂点への距離の積が $m$ になる』 という命題でした。 円弧を $m$ 等分した点からの距離の積を考えると、$m$ によらない値がでてくるんですね。
正5角形、$ P_2$ の場合
正5角形、$ P_6$ の場合
\[ \prod^{m-1}_{k=0} 2\sin\left(x+\frac{k}{m}\pi\right) = 2\sin mx \tag{a}\] から \[ \prod^{m-1}_{k=0}\left\{ \left( \cos 2x - \cos \frac{2k}{m}\pi \right)^2 + \left( \sin 2x - \sin \frac{2k}{m}\pi \right)^2 \right\} = 4\sin^2 mx\tag{b}\] が導かれることを示します。
(b)の左辺について、積 $k$ のとる範囲を $0$ から $-m+1$ に変えても値は同じなので、 \[ 左辺 = \prod^{m-1}_{k=0}\left\{ \left( \cos 2x - \cos \frac{-2k}{m}\pi \right)^2 + \left( \sin 2x - \sin \frac{-2k}{m}\pi \right)^2 \right\}\] 中括弧の中は \begin{align} &\cos^2 2x -2\cos 2x \cos \frac{2k}{m}\pi + \cos^2 \frac{2k}{m}\pi + \sin^2 2x +2\sin 2x \sin \frac{2k}{m}\pi + \sin^2 \frac{2k}{m}\pi\\ &=2-2\cos\left( 2x+\frac{2k}{m}\pi \right)\\ &=4 \sin^2\left(x+\frac{k}{m}\pi\right) \end{align} よって(b)は \[ \left(\prod^{m-1}_{k=0} 2\sin\left(x+\frac{k}{m}\pi\right)\right)^2 = 4\sin^2 mx \] と同値であり、等式(a)は十分条件になります。
等式(2)
\[ 2\sin (mx) = \prod^{m-1}_{k=0} 2\sin \left( x+\frac{k}{m}\pi\right)\]
の両辺を改めて見てみると、両辺が $0$ となる $x$ の集合が
\[ \left\{ \frac{k}{m}\pi\ \middle|\ k\in\mathbb{Z} \right\} \]
として一致していることがわかります。そこで $\sin$ の無限積公式
\[ \sin\pi x = \pi x \prod_{n\neq 0}\left( 1+\frac{x}{n}\right)\]
を使って示せるのではないかと考えた所、なんとなくつながったので以下にご紹介します。
なおこの証明では最初の等式を特殊化した等式
\[ m = \prod^{m-1}_{k=1} 2\sin \left( \frac{k}{m}\pi\right) \]
を使います。
\begin{align} \sin m\pi x &= m\pi x \prod_{n\neq 0}\left( 1+\frac{m}{n}x\right)\\ &= m\pi x \prod_{l\neq 0}\left( 1+\frac{m}{(ml)}x\right)\times \prod_{k=1}^{m-1}\prod_{l}\left( 1+\frac{m}{(ml+k)}x\right)\\ &= m\pi x \prod_{l\neq 0}\left( 1+\frac{1}{l}x\right)\times \prod_{k=1}^{m-1}\prod_{l}\left( \frac{ml+k+mx}{ml+k}\right)\\ &= m\sin (\pi x)\times \prod_{k=1}^{m-1}\prod_{l}\left( \frac{ml+k+mx}{ml+k}\right)\\ &=m\sin (\pi x)\times I\\ \end{align} とすると \begin{align} I &= \prod_{k=1}^{m-1}\prod_{l}\left( \frac{ml+k+mx}{ml+k}\right)\\ &= \prod_{k=1}^{m-1}\frac{k+mx}{k}\prod_{l\neq 0}\left( \frac{ml}{ml+k}\times\frac{ml+k+mx}{ml}\right)\\ &= \prod_{k=1}^{m-1}\frac{k/m+x}{k/m}\prod_{l\neq 0}\left( \left(1+\frac{k}{ml}\right)^{-1}\times\left( 1+\frac{k/m+x}{l}\right)\right)\\ &= \prod_{k=1}^{m-1}\frac{k/m+x}{k/m}\prod_{l\neq 0}\left( \left(1+\frac{k}{ml}\right)^{-1}\times\left( 1+\frac{k/m+x}{l}\right)\right)\\ \end{align} よって $s=k/m$ と置くと \[ I =\frac{\prod_{k=1}^{m-1} \pi (s+x) \prod_{l\neq 0}\left( 1+\frac{s+x}{l} \right)}{\prod_{k=1}^{m-1}\pi s \prod_{l\neq 0}\left( 1+\frac{s}{l} \right) }=\frac{\prod_{k=1}^{m-1}\sin (\pi (x+s))}{\prod_{k=1}^{m-1}\sin (\pi s)}\] これの分母は \[ \prod_{k=1}^{m-1}\sin (\pi s)=\prod_{k=1}^{m-1}\sin \left( \pi \frac{k}{m}\right) = \frac{m}{2^{m-1}}\] なので、結局 \[ I =\frac{1}{m}\prod_{k=1}^{m-1}2\sin (\pi (x+s))\] 以上から \[ 2 \sin m\pi x = \prod_{k=0}^{m-1} 2\sin\left(\pi x+\frac{k}{m}\pi\right)\] が示せました。(証明終わり)