関数 $f(x)$ と、複素数 $u\neq 0$ に対して、 \[ \delta_n(u) \cdot f(x) :=\frac{1}{u} \sum_{k=0}^n (-1)^k \binom{n}{k} f(x + uk) \] \[ D(u) \cdot f(x) := -\sum_{n=1}^{\infty}\frac{1}{n}\ \delta_n(u) f(x) \] とする。
複素数 $a$ に対して $ ua=x+yi,\ x,y\in\mathbb{R}$ としたとき、 \[ e^{x}<2\cos y,\ -\frac{\pi}{2} < y < \frac{\pi}{2}\] ならば、 \[ D(u)\ e^{ax} = a\ e^{ax}\]
\begin{align} \delta_n(u)\ e^{ax} &=\frac{1}{u} \sum_{k=0}^n (-1)^k \binom{n}{k} e^{a(x+ uk)}\\[10px] &=\frac{1}{u}\left( \sum_{k=0}^n \binom{n}{k} \left(-e^{ua}\right)^k \right) e^{ax}\\[10px] &=\frac{ \left( 1-e^{ua} \right)^n}{u} \cdot e^{ax} \end{align} よって \[ D(u) e^{ax} =- \frac{1}{u} \left( \sum_{n=1}^{\infty}\frac{(1-e^{ua})^n}{n} \right) e^{ax} \] $|1-x |<1$ のとき、 \[ \log(x) = -\sum_{n=1}^\infty \frac{(1-x)^n}{n} \] \[ -\frac{\pi}{2} < \mathrm{Im} \left( \log(x) \right) < \frac{\pi}{2}\] よって、 $e^{x}<2\cos y$ のとき $|1-e^{ ua} |<1$ なので \[ D(u) e^{ax} = \frac{1}{u} \log(e^{ ua})\cdot e^{ax}\] \[ -\frac{\pi}{2} < \mathrm{Im} \left( ua \right) < \frac{\pi}{2}\] のとき、 \[ \log(e^{ ua})=ua\] なので、 \[ D(u) e^{ax} = a e^{ax}\]
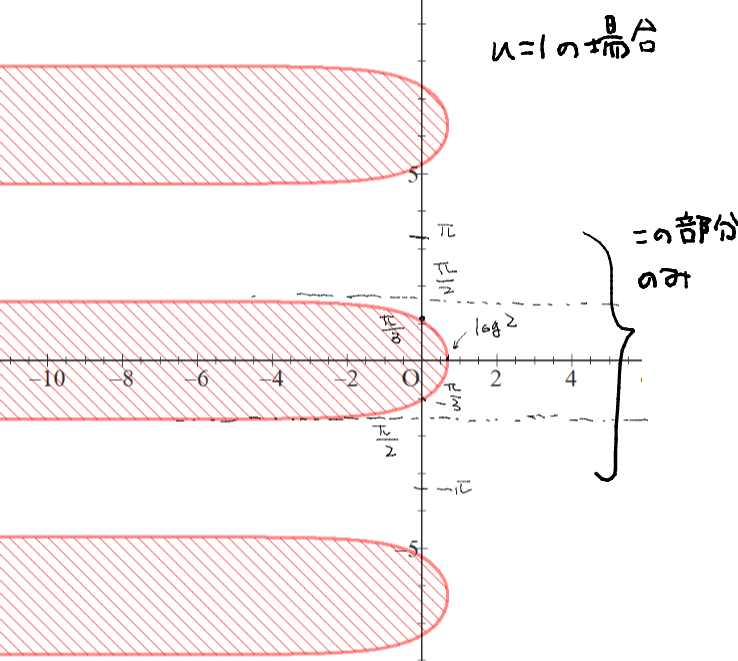
$u=1$ の場合の条件を満たす $a$ の範囲
